Range Search is a very basic alogorithm used in multiple situations, like out of a set of 100 employees, find all whose salary falls between a specific range. As we are talking about sigle aspect (salary), we will use a 1-D range serach approach to solve this problem.
A simple algorithm would use a Balanced binary serach tree, with property that all the nodes in left subtree are smaller than root node and all right subtree node are higher, for any subtree. The balancing property make sure all the root nodes are at a distance on X or X-1, where X is order of lg(N), N being nodes in tree.
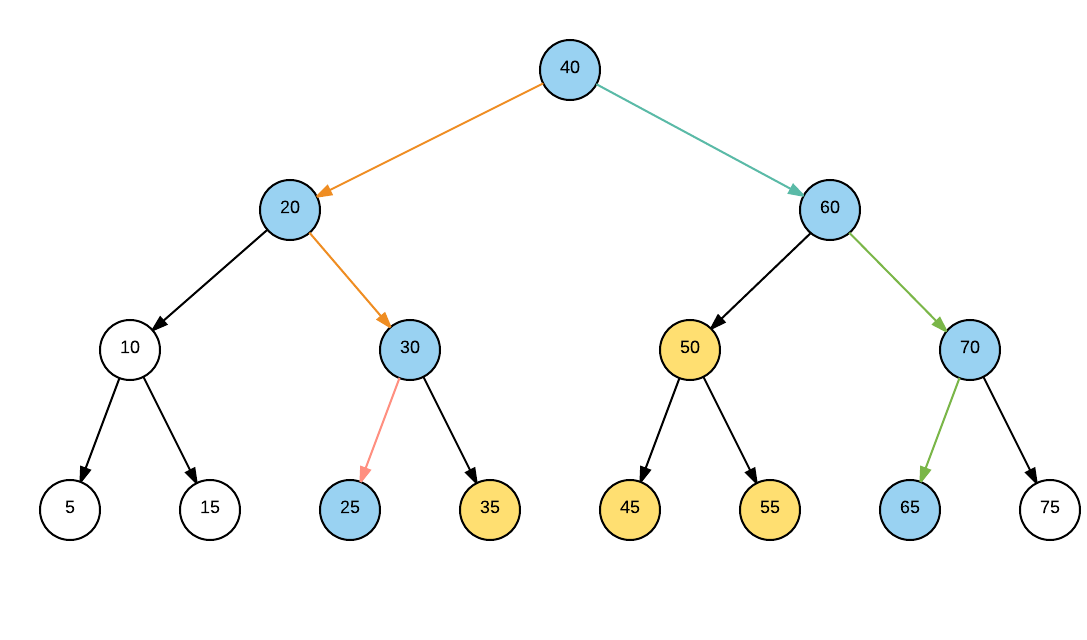
Here is an example
Lets say the number represent salary of employess in thousands. And the range we need to find is say 23 and 63. We will traverse tree for both lower and upper bound. Orange arrows signifies traversal for 23 and Green ones show traversal for 63.
This leaves us with three type of nodes.
1. Nodes not traversed and lie out of subrees of traversal path (white nodes)- can be ignored
2. Nodes in path of traversal (blue nodes)- may or may not be in range
3. Node lying between traversal path (Yellow nodes)- these are in range.
Using above information, we can deduce a simple algorithm
1. Input lower range L, and high range H
2. Create a output set S as range set
3. Traverse/ search for L in the tree (if L is smaller than node, move right, else move left)
3a. if the node being traversed is in range, add to set S
3b. If L is less than Node value, Add the whole right subtree of current node to the set S (as it is in range)
4. Traverse/ search for H in the tree (if H is smaller than node, move right, else move left)
4a. If the node being traversed is in range, add to set S
4b. If H is greater than Node value, Add the whole left subtree to the set S (as it is in range)