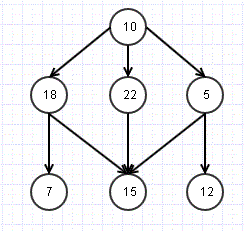
Breadth First search is an effective search mechanism for Graphs and Tree Data structure. As the name suggest, this technique makes sure that all the nodes at same level/ breadth are checked before moving to deeper levels.
The above structure is hybrid of tree and graph (Still a tree as there are no cycles). Let us what it means to do a breadth first search here.
We will start with root node i.e. 10.
Move to level 2 and check nodes 18, 22, 5.
Check the next level- 7, 15, 12 and so on.
Here is algorithm to implement Breadth first search
1. Add root node R to queue- Q
2. Fetch next node N from Q
3 a. If the N.val is required val, return success
3 b. Else Find all Child/ Neighbour nodes which are not traversed already and add to Queue
4. If there are more nodes in Q, Repeat from 2.
5. If Q is empty, we know we have traversed all nodes, return failure as node not found
Read more here- http://en.wikipedia.org/wiki/Breadth-first_search
http://en.wikipedia.org/wiki/Breadth-first_search