At times people confuse between terms Data Analysis and Data Science. We can think of these as
Data Analysis– Analyze the historical data to extract information like fraud detection.
Data Science– Data science take it to next step and use learnings to build a predictive model for example detect future frauds and trigger alerts.
Machine learning in its simplest form can be think of writing code or algorithms, so that we can make machine to learn from provided inputs and deduce conclusions.
Some of the ML use cases are
– Automated personal voice assistants like siri (includes NLP natural language processing)
– Identify investment opportunities in trading by analysing data and trends
– Identify high risk or fraud cases
– Personalize shopping experience by learning from users purchasing patterns
Types of Machine learnings: We can divide use cases in three broad categories
Supervised
Unsupervised
Reinforcement
Supervised Learning: Historical data is used and algorithms are worked out for predictive analysis. The historical data is usually divided into training dataset and test dataset. Machine learning techniques are applied on training dataset and a model is created. Than this model is tested on test dataset to validate the accuracy of the model generated. When a satisfactory model/ set of rules are finalized, this is used to predict future transactions outcome.
One example of supervised learning is, you have sample data for last few years for employee attrition. Data captured for employees is experience level, salary related to industry, last promotion, weekly working hours etc. Using the historical data, a predictive model (or formula) is created, which can point out to key factors which triggers an employee leaving the company and also can predict how likely is someone leaving the company in next 1 year.
Common Supervised learning algorithms:
Linear Regression: This is used to estimate real values for example prices of commodities, sales amount etc. Existing data is looked as points on dimensional graph and a linear pattern is found (think of a formula being created ax+by+c). The data to be predicted is then provided to the model and expected values are calculated.
Logistic Regressions: Somewhat similar to linear regression but we are looking for true or false decision based answers.
Decision Tree: Used for classification problems. Think as if you have N numbers of buckets of labels available, and you need to figure out to which bucket the given object belongs to. A series of decisions are taken to find correct bucket. e.g, taking the employee attrition example above, we have 2 buckets, employee will leave company in next one year or not leave. The decision tree questions can be, Was employee promoted this year, If Yes, add to not leave else if employee got good appraisal rating, if no add to leave bucket and so on.
Random Forest: Advanced or cluster of decision trees for better analysis. In decision tree we followed one series of question, but the tree itself can be created in multiple ways. Hence Random forest consider these multiple trees and find the classification.
Naive Bayes Classifier: Bayes theorem (conditional probability) based classification.
SVM or Support Vector Machines: Mostly used in classification problems, this tries to divide dataset into groups and than tries to find out a hyperplane which will divide the objects in the group. For example, for a 2 dimensional characterisation, a hyperplane is a line, whereas in 3 dimension, it will be a plane.
Once we have predictive model ready, we look at confusion matrix to help us understand the accuracy. Confusion matrix is a 2*2 Matrix
[ [T.P, F.P]
[F.N, T.N] ]
Where T.P is true positive, F.P. is false positive, F.N. is false negative and T.N. is true negative. The confusion matrix gives us success percentage for our model.
Unsupervised Learning: The difference between supervised and unsupervised learning is that in supervised learning we had buckets or labels already available and we were required to assign the data. In unsupervised learning, we are just provided with data and we need to find out classifications or buckets. Or in simple words we need to cluster the objects meaningfully.
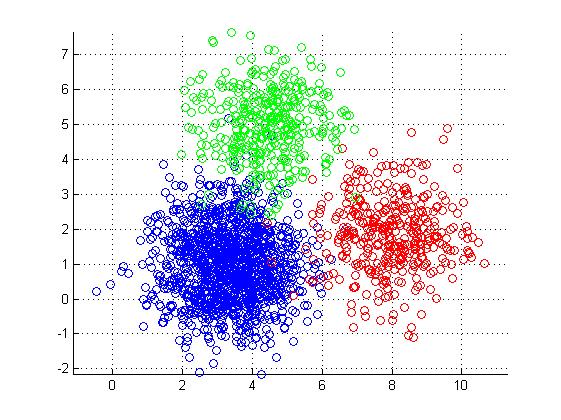
A use case can be you are provided with a number of objects (say fruits), now you have to classify these into groups. We can do it on based on different parameters such as shape, size, color etc.
Common clustering techniques
K-means: This is about clustering or dividing objects into K groups. Refer http://kamalmeet.com/machine-learning/k-means-clustering/
C-means or Fuzzy clustering: In K means we tried to make sure that an object is strictly part of a group, but this might not be possible always. C-means clustering allows some level of overlap between clusters, so an object can be 40% in one cluster and 60% in other.
Hierarchical: As the name suggests clusters have parent child relationship and we can think of clusters as a part of hierarchical tree. Start by putting each object as individual cluster (leaf nodes) and than start combining logical cluster under one parent cluster. Repeating the process, will give us final clustering tree. For example, Orange is part of citrus fruits, which say belongs to juicy fruits, which further belongs to Fruits as top cluster.
Reinforcement Learning: In the above two learnings, we have supplied the machine information about how to come up with a solution. Reinforcement learning is different as we expect machine to learn from its experience. A reward and penalty system is in place to let machine know if the decision made was correct or incorrect to help in future decisions.
Helpful links:
https://www.analyticsvidhya.com/blog/2017/09/common-machine-learning-algorithms/