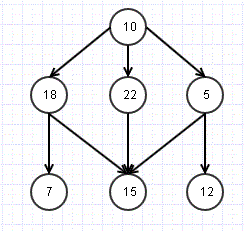
In last post I talked about Breadth First Search. An alternative to that, is Depth First Search, used in cases we want to check upto a depth level first rather than breadth.
So let’s look back at the last example
This time we would like to parse something like
1. Check Root- 10
2. Check till depth level for one node- 18,7
3. Repeat for other nodes 22,15 and then 5, 12
A straight forward way is to modify the Breadth First Search algorithm to use Stack instead of Queue.
1. Push Root Node R to Stack S
2. Pop s node from S
3 a . If s.val is required value, return Success
3 b. Else Push all Neighbor/ child nodes to stack
4. If Stack is not empty, Repeat from 2
5. If Stack is empty, we have traversed all the nodes and not found the required node. Return failure.