Heap sort is one of the most important and interesting algorithms. The implementation is base of many other sophisticated algorithms. We will focus on basics of heap sorting here. Infact, if you understand what a heap data structure is, heap sort is just application of some known simple operations on the heap.
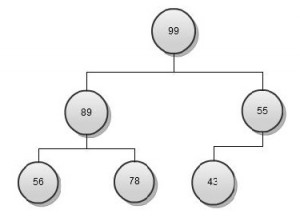
Let’s relook at our heap
This is a max heap so let’s try to create an array in reverse sorted order (a min heap is good for sorted in lowest to highest format and vice versa). Before moving forward, revisit the heap data structure and understand Insert and Delete operations, after that heap sort algorithm is a cake walk.
We know that max heap has a property that element at the top is highest. Using this property, we can create an algorithm like
- Create max heap from the random array
- Remove top element from heap and add to reverse sorted array
- Heapify (restore heap property) the remaining heap elements
- Repeat Step 2 till the heap is empty
Step 1 is nothing but inserting all elements of an array to heap. One Insert Key operation takes Log N operations so N elements will take N Log N
Step 2 is order of 1 as we are just removing the top element and adding to our array
Step 3 is nothing but Delete Node operation in heap, i.e. take last leaf node and add as root, then compare with its child nodes and swap with largest. Repeat the process till heap property is maintained, i.e. child is greater than parent. This is Log N operations for one heapify.
Step 4 is combination of 2 & 3, N times. Step 2 is constant order and hence can be ignored. This means we have N Step 3 order or N Log N.
Combining Step 1 and 4, we figure out order of heap sort complexity is of N Log N order.