If we look at wikipedia for Prim’s alogorithm, it states

“Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph”

https://en.wikipedia.org/wiki/Prim%27s_algorithm

Let’s take this line word by word

Greedy algorithm: means this algorithm looks at the best option available at current stage and move stage by stage.

weighted graph: a graph where edges have a weight associated, for example distance as weight in case of a graph showing path between cities.

undirected graph: A graph which does not worry about direction of edges. A edge between vertices A and B would mean it can travel both ways.

Minimum spanning tree: In a graph, a minimum spanning tress is a tree, which has only edges which are required to connect all the nodes and keeping minimum weight.

Now Coming to Prim’s algo, again using wikipedia’s definition

    1. Initialize a tree with a single vertex, chosen arbitrarily from the graph.
    2. Grow the tree by one edge: of the edges that connect the tree to vertices not yet in the tree, find the minimum-weight edge, and transfer it to the tree.
    3. Repeat step 2 (until all vertices are in the tree).

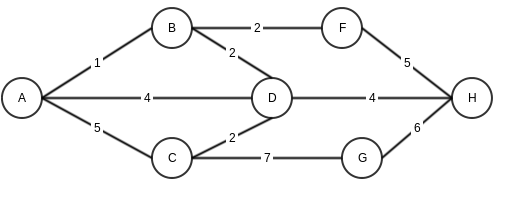
Let’s say we have a graph

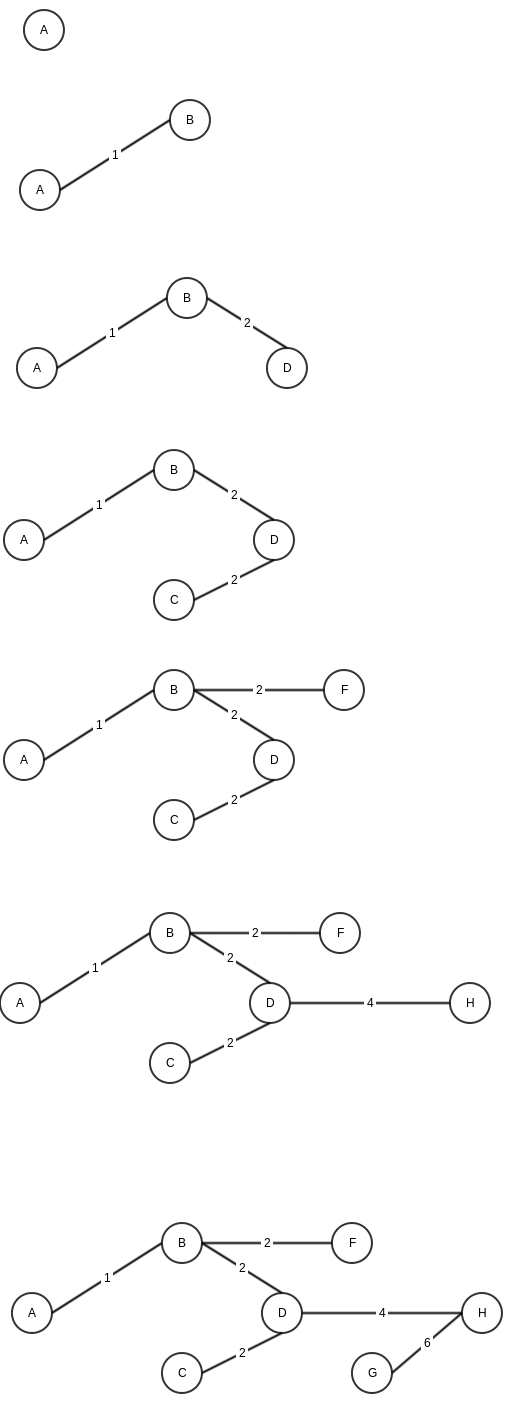
Here is step by step execution of Prim’s algorithm (note that for steps where we have multiple same minimum weight options, I am choosing randomly)