In last post I mentioned about Binary Search tree. One challenge with Binary Search Tree or BST is when we try to insert a sorted list into it, we will end up a straight list structure rather than tree, i.e. we are adding all the nodes to one side. For example

In this case, when we search for an element at extreme right, we are making O(N) comparisons.

To improve this situation, we have Balanced Binary search trees. AVL is one of such Balanced BST trees.

AVL tree has additional property over BST, that at any point of time, any 2 subtrees from a root can differ in height by order of 1. Or in other words, in a tree with height N, only last 2 level (N and N-1) of the tree can have leaf nodes without children.

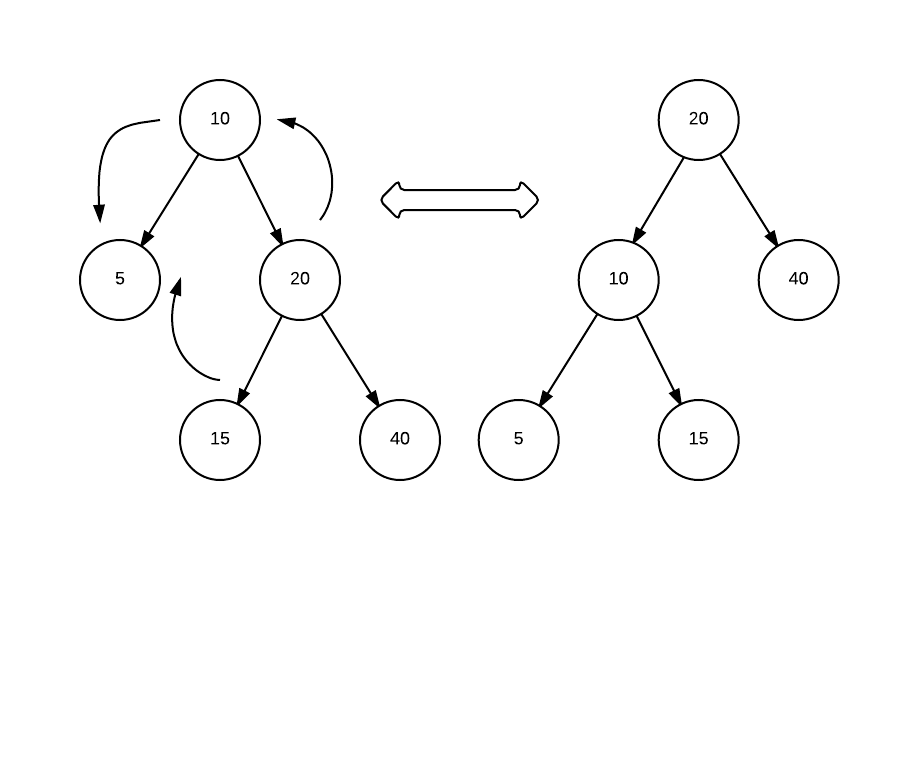
AVL Tree maintains this balance using tree rotation. We can rotate a tree (or subtree) in left or right direction.

The above example shows how left rotation works (if you look other way around, swap source and destination, it is right rotation).

More on tree rotation- https://en.wikipedia.org/wiki/Tree_rotation

Additional reads
https://en.wikipedia.org/wiki/AVL_tree

http://www.geeksforgeeks.org/avl-tree-set-1-insertion/

http://stackoverflow.com/questions/14670770/binary-search-tree-over-avl-tree

A very good visual representation of AVL tree Vs Binary tree. Try creating a tree with nodes 1,2,3,4,5,6,7,8,9 and see visual difference between 2 trees. http://visualgo.net/bst.html#