Graph is distant relative of Tree. Infact it is complexer than tree, as in tree, a node usually have link with nodes one level up or down and does not conatin any cycles, whereas graph does not have any such restrictions. Graph data structure is more useful in case of something like traveling salesman problem, or to represent computer network, i.e. a structure where we have nodes and relationship between them.

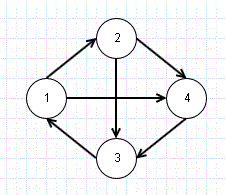
In the above graph structure, we have 4 nodes or Vertices and 6 Edges (connectors). A graph is usually represented as G=(V,E).

Please note that the graph given above is directed, that is we can see link is from 1->2 and not 2->1. In undirected graph, the arrows showing direction of connection will not be there and connection can be considered both ways.

Adjacency Matrix

The above graph can be shown as

[1] [2] [3] [4]
[1]   0    1     0    1
[2] 0 0 1 1
[3] 1 0 0 0
[4] 0 0 1 0

if the same graph was undirected
[1] [2] [3] [4]
[1] 0 1 1 1
[2] 1 0 1 1
[3] 1 1 0 1
[4] 1 1 1 0

Always Aij=Aji in undirected

Adjacency List Representation

Node1->[Node2, Node4]
Node2->[Node3, Node4]
Node3->[Node1]
Node4->[Node3]

Other useful information for Graphs

Degree: Number of edges being attached to current vertex
In-Degree: Number of edges coming into the vertex in case of directed graph
Out-Degree: Number of edges going out from the vertex in case of directed graph

Weighted Graphs:

This is important in case we are trying to solve problems like traveling salesman. For example, if we look at above graph, we can see there are 2 ways to reach Vertex 3 from Vertex 1, that is, 1->4 or 1->2->4. Say these vertices represent cities, and edge weight represent distance in this case.

1->2= weight 20
2->4= 30
1->4= 60

So we can choose 1->2->4 over 1->4 as it will be shorter distance.