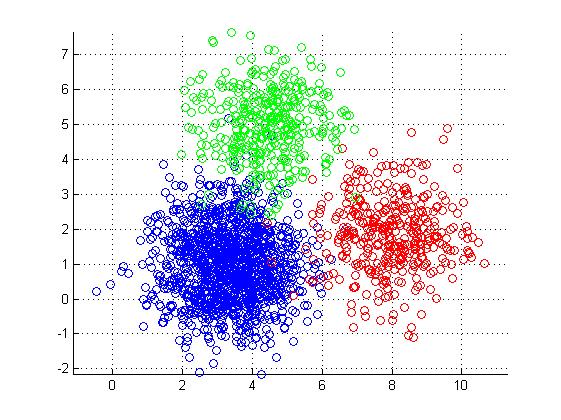
Clustering, as the name suggest is simply grouping some random elements. Say, you are given points on a 2-D graph, you need to figure out some kind of relationship or pattern among them. For example you might have crime position in a city or Age vs Mobile Price graph for purchasing habit of an online website.
In Machine Learning, clustering is an important class of algorithms as it helps figure out a pattern in random set of data and helps take decision based on the outcome. For example, an online store needs to send a targeted marketing campaign for new Mobile phone launched. Clustering algorithm can help figure out buying patterns and single out customers who are most likely to buy the mobile phone launched.
There are many clustering algorithms, K-means being one of the simplest and highly used.
1. Place K points randomly on the graph. These will serve as initial center points or centroids of the K clusters.
2. Now assign each item (point) existing in the graph to one K clusters, based on its closeness (shortest distance from centroid) to the centroid of cluster
3. When all items are assigned a cluster, recalculate centroid of the cluster (point from where distance to all the items in cluster is minimum on an average).
4. Repeat step 2 and 3, until there is no scope of improvement (no movement in seen in centroids).
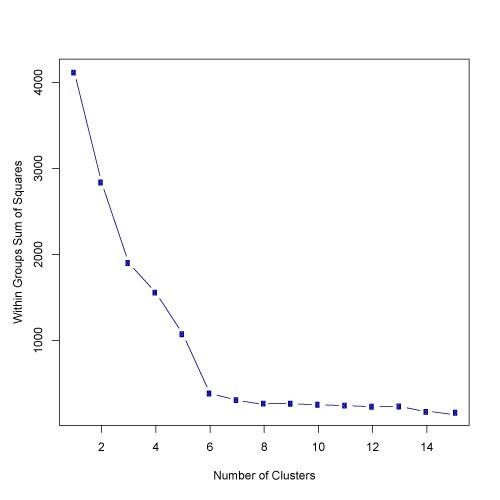
The above algorithm will divide all the items into K clusters. Another challenge will be to come up with optimum value of K. i.e. How many clusters can correctly or adequately represent the data. Well there are many ways to figure that, one of effective way is the elbow method. You start plotting number of clusters on X axis and Sum of squared errors on Y axis. Sum of squared errors is, you take each point in a cluster, find the distance from centroid and square it (to eliminate negative distances), this is the error for this particular point as ideally you want each point near to centroid of cluster to make it perfect. Then sum up all these errors and plot on graph. The resulting graph starts looking like an arm. We find out the elbow, that is, where we see the numbers getting flatter on X axis. This means any additional cluster is not adding too much value to the information we already have.