A few days back I wrote about the basics of decision making. Next, we will look into Sensitivity analysis.
Sensitivity Analysis examines how our decision might change with different input data.
We will start with our previous example, where a company is trying to launch a product and they have the following options right now.
| ALTERNATIVE | SUCCESS OUTCOME | FAILURE OUTCOME |
|---|---|---|
| Go with prototype 1 | 200,000 | -180,000 |
| Go with prototype 2 | 100,000 | -20,000 |
| Do nothing | 0 | 0 |
Let us say
P = Probability of a favourable market i.e. Success
(1-P) = Probability of unfavourable market i.e. failure
Sensitivity Analysis
EMV Prototype 1 = 200000P – 180000(1-P)
= 380000P – 180000
EMV Prototype 2 = 100000P – 20000(1-P)
= 120000P – 20000
EMV Do nothing = 0P – 0(1-P) = 0
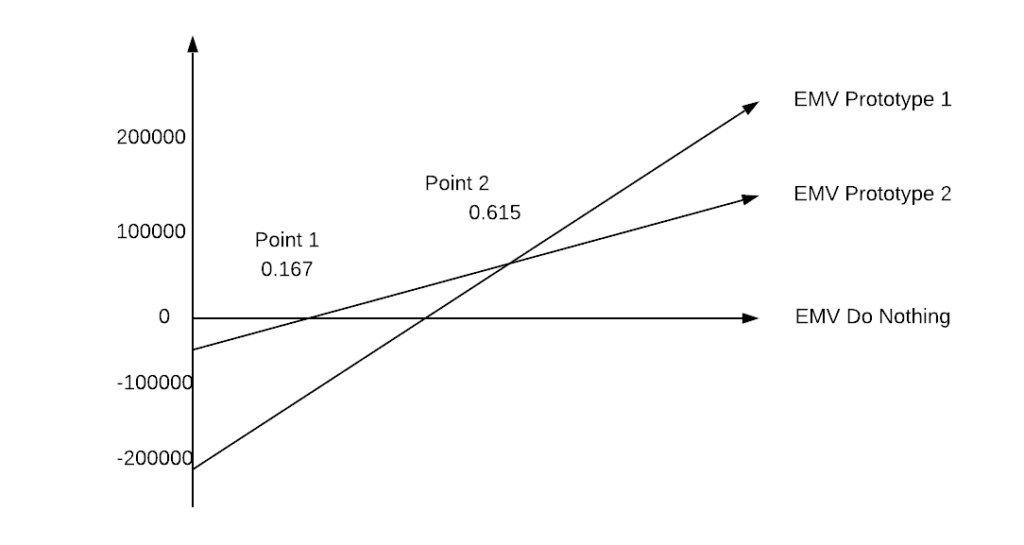
Point 1
EMV Do nothing = EMV Prototype 2
0 = 120000P – 20000
P = 20000/120000
P = 0.167
Point 2
EMV Prototype 2 = EMV Prototype 1
120000P – 20000 = 380000P – 180000
P = 160000/260000
P = 0.615
So based on sensitivity analysis we can conclude based on probability of success or favorable market P, that
Do nothing if P < 0.167
Go for prototype 1 if P>=0.167 and P<0.615
Go for Prototype 2 if P>= 0.615
